Cultivar el interés de los niños por las matemáticas y mejorar sus habilidades matemáticas siempre ha sido una preocupación importante para los padres. Estudiar para la Olimpiada Internacional de Matemáticas (OIM) es un método muy eficaz. La OIM no solo requiere que los estudiantes comprendan a fondo conceptos matemáticos complejos como álgebra, geometría y teoría de números, sino que también cultiva su capacidad para resolver problemas. Este aprendizaje también ayuda a desarrollar el pensamiento lógico de los niños, permitiéndoles pensar de forma independiente, ejercitar el pensamiento creativo y resolver problemas. Todas estas habilidades de pensamiento lógico son extremadamente valiosas en la vida diaria y la investigación académica.
Los problemas de matemáticas de las olimpiadas suelen ser bastante desafiantes, pero los niños adquieren una enorme sensación de logro y confianza al resolverlos con éxito. Esta experiencia de éxito los motiva a seguir aprendiendo y a alcanzar mayores logros en otras áreas. En general, aprender matemáticas de las olimpiadas no solo les ayuda a construir una base matemática sólida, sino que también cultiva importantes habilidades de pensamiento lógico, a la vez que aumenta su confianza y amplía sus conocimientos.
Actualmente existen diversas clases de matemáticas olímpicas y programas de matemáticas olímpicas para preescolares, que permiten a los niños participar y desafiarse con problemas matemáticos olímpicos. A continuación, se presentan algunas recomendaciones de clases de matemáticas olímpicas populares: [Información sobre clases de matemáticas olímpicas populares].
Problemas de olimpiadas de matemáticas para estudiantes en transición de primero a segundo grado.
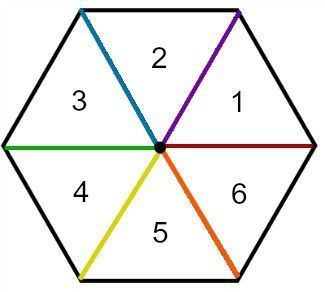
Este es un problema de competencia de matemáticas del examen de admisión de primero a segundo grado: Un reloj se rompió en tres pedazos, y la suma de los números en cada pedazo es exactamente la misma. ¿Sabes cómo se rompió el reloj? 😙
Se cayó un reloj y se rompió en tres pedazos, cada uno con la suma de los números igual. ¿Sabes qué forma adquirió el reloj? 😙

Primero, los niños deben sumar los números del 1 al 12: 1 2 ... 12 = 78. Luego, dividen 78 entre 3 para obtener 26. Sabemos que el número total de cada parte del reloj es 26. Entonces, niños, ¿saben si el reloj está dividido en forma de "人" (humano) o de "二" (dos)? 😘
(Olimpiada de matemáticas de jardín de infantes)
Problemas de Olimpiada de Matemáticas para estudiantes en transición de segundo a tercer grado
Este es un problema de competencia de matemáticas para alumnos de segundo a tercer grado. El problema requiere que los niños dividan 6 tarjetas numéricas en tres grupos de modo que la suma de los números en cada grupo sea la misma. ¿Qué método puedes usar fácilmente para resolverlo? 😙
Hay 6 cartas sobre la mesa. Ella, Tommy y Sarah reciben 2 cartas cada uno. ¿Cuáles son los tres conjuntos de cartas si la suma de los números de todas las cartas en sus manos debe ser la misma?

En nuestras clases competitivas de olimpiadas de matemáticas, enseñamos conceptos matemáticos muy prácticos, como operaciones relacionadas. Al usar con destreza la suma, la resta y la relatividad, podrás encontrar fácilmente las respuestas. ✨
Primero, divide los números en dos grupos según su tamaño: un grupo grande (6, 7, 8) y un grupo pequeño (3, 4, 5), y ordénalos del mayor al menor.
Empareje el número más grande (8) del grupo más grande con el número más pequeño (3) del grupo más pequeño.
8 3 = 11
Empareje el número más pequeño (6) del grupo más grande con el número más grande (5) del grupo más pequeño.
6 5 = 11
Empareje el número del medio del grupo más grande (7) con el número del medio del grupo más pequeño (4).
7 4 = 11
¿Lo entiendes? 😉
(Olimpiada de matemáticas de jardín de infantes)
Problemas de olimpiadas de matemáticas para estudiantes en transición de tercero a cuarto grado
Este es un problema de competencia de matemáticas del examen de admisión de 3.º a 4.º grado. El buey y la rata se enamoraron y se casaron, con el gallo como sacerdote. De repente, apareció un animal y detuvo la boda. En el caos, se vieron cuatro animales con diez patas en el escenario principal. ¿Cuál de los 12 animales del zodíaco detuvo la boda? 😙
La Vaca y el Ratón se enamoraron y se casaron. El Pollo fue el sacerdote de su boda. De repente, apareció un animal para detener el caos de la boda. En el escenario principal, había 4 animales con un total de 10 patas. ¿Qué animal de los 12 signos del zodíaco interrumpió la boda? 🐭 🐮 🐔

Problemas de Olimpiada de Matemáticas para estudiantes en transición de cuarto a quinto grado
Este es un problema de competencia de matemáticas de cuarto a quinto grado, donde comienzas a usar fracciones para resolver el problema. 😙
El número de estanterías rojas es 1/3 del número de estanterías verdes. El número de libros en cada estantería roja es 1/4 del número de libros en cada estantería verde. Cada estantería verde tiene 4 libros, y no hay 4 estanterías rojas en total. ¿Cuántos libros hay en total en las estanterías roja y verde?

El problema establece que hay 4 estanterías rojas 🟥🟥🟥🟥, y el número de estanterías rojas es 1/3 del número de estanterías verdes.
Por lo tanto, hay 12 estanterías verdes. 🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩
🟩Cada estantería verde tiene 4 libros📙📙📙📙, mientras que cada estantería roja tiene 1/4 del número de libros que cada estantería verde.
🟥Entonces cada estantería roja tiene 1 libro📔.
No es muy difícil, ¿verdad? 😁
(Olimpiada de matemáticas de jardín de infantes)
Problemas de la Olimpiada de Matemáticas de Kindergarten K2
Problemas de la Olimpiada de Matemáticas de Kindergarten K3
Este es un problema de competición de matemáticas de nivel 1 de kínder (preescolar). El problema de la boda que aparece a continuación no es algo que ni siquiera los adultos puedan resolver de inmediato. 😙
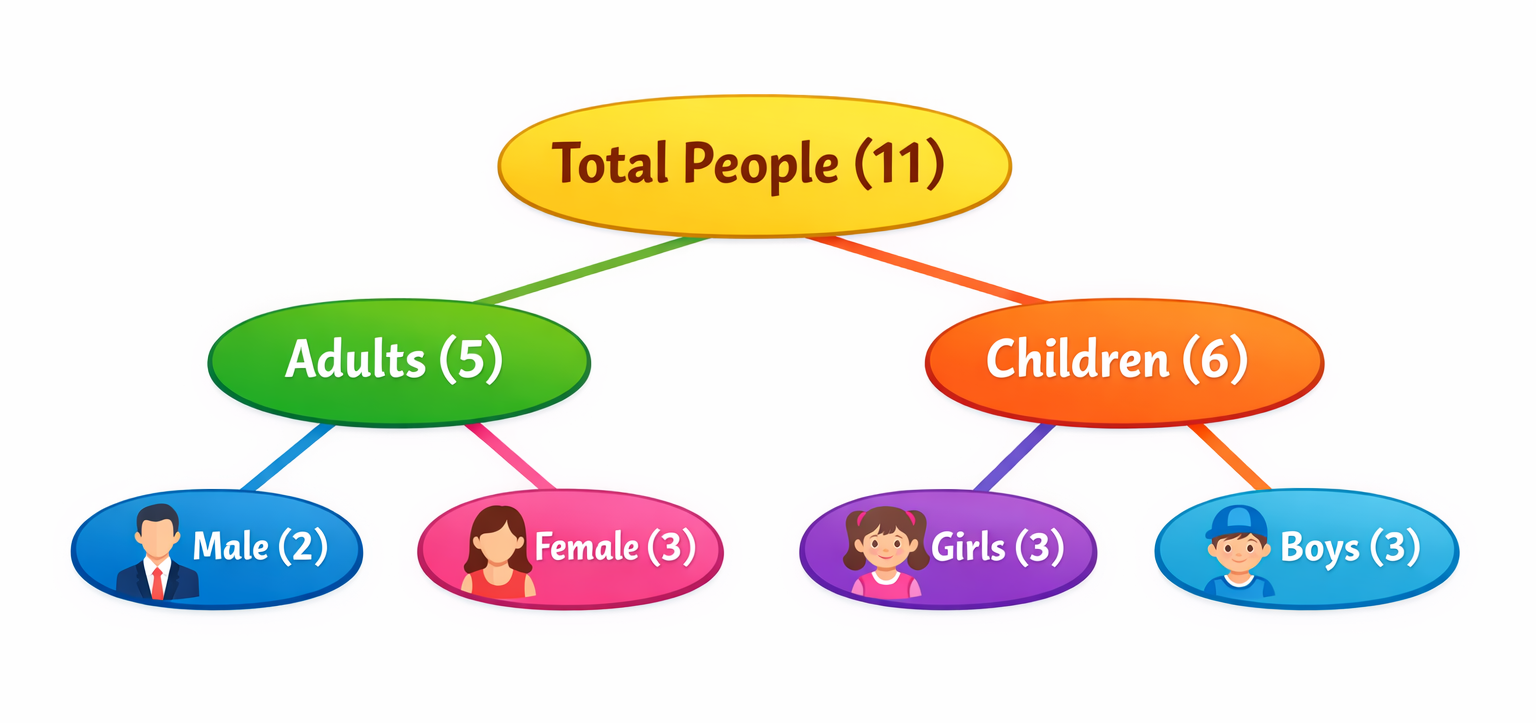
Suki asiste a una boda. Había personas presentes, cinco de ellas adultas. Suki encontró a tres niñas y dos hombres adultos. ¿Cuántas mujeres adultas hay en la boda? ¿Y cuántos niños?

En nuestra olimpiada de matemáticas de nivel competitivo (olimpiada de matemáticas preescolar), enseñamos a los niños a usar diferentes métodos para intentar deducir la respuesta. ✨
Podemos hacer que los niños dibujen una tabla, con los niños a la izquierda y las niñas a la derecha, los adultos arriba y los niños abajo, luego insertar los números relevantes para deducir la respuesta. 😉