[Olympiad Math Problems] Free download of Olympiad Math practice problems detailed video explanations (Part 2)

Cultivating children's strong interest in mathematics and improving their mathematical abilities has always been an important concern for parents. Studying for the International Mathematical Olympiad (IMO) is a highly effective method. IMO not only requires students to deeply understand complex mathematical concepts such as algebra, geometry, and number theory, but also cultivates their problem-solving abilities. This learning also helps develop children's logical thinking, enabling them to think independently, exercise creative thinking, and solve problems. These are all extremely valuable logical thinking skills in daily life and academic research.

Olympiad math problems are often quite challenging, but children gain a tremendous sense of accomplishment and confidence when they successfully solve them. This experience of success helps motivate children to continue learning and achieve greater success in other areas. Overall, learning Olympiad math not only helps build a solid mathematical foundation but also cultivates important logical thinking skills, while boosting their confidence and broadening their knowledge.

There are now various Olympiad math classes and preschool Olympiad math programs available on the market, allowing children to participate in and challenge themselves with Olympiad math problems. Below are some recommendations for popular Olympiad math classes: [Provides information on popular Olympiad math classes].

First, children need to add up the numbers from 1 to 12: 1 2 ... 12 = 78. Then, divide 78 by 3 to get 26. We know that the total number of each part of the clock is 26. So, children, do you know if the clock is split in a "人" (human) shape or a "二" (two) shape? 😘

(Kindergarten Math Olympiad)

Math Olympiad problems for students transitioning from second to third grade

This is a math competition problem for second to third graders. The problem requires children to divide 6 number cards into three groups so that the sum of the numbers in each group is the same. What method can you easily use to solve this? 😙

There are 6 cards on the table. Ella, Tommy, and Sarah each receive 2 cards. What are the three sets of cards if the sum of the numbers on all the cards in their hands must be the same?

In our competitive math Olympiad classes, we teach some very practical mathematical concepts, such as related facts. By skillfully using addition, subtraction, and relativity, you can easily find the answers. ✨

First, divide the numbers into two groups based on their size: a large group (6, 7, 8) and a small group (3, 4, 5), and arrange them from largest to smallest.

Pair the largest number (8) in the larger group with the smallest number (3) in the smaller group.

8 3 = 11

Pair the smallest number (6) in the larger group with the largest number (5) in the smaller group.

6 5 = 11

Pair the middle number of the larger group (7) with the middle number of the smaller group (4).

7 4 = 11

Do you understand? 😉

(Kindergarten Math Olympiad)

Math Olympiad problems for students transitioning from third to fourth grade

This is a math competition problem from the 3rd to 4th grade entrance exam. The ox and the rat fell in love and got married, with the rooster acting as the wedding priest. Suddenly, an animal appeared and stopped the wedding. In the chaos, 4 animals with 10 legs were seen on the main stage. Which of the 12 zodiac animals stopped the wedding? 😙

Cow and Mouse fell in love and got married. Chicken became the priest for their wedding. Suddenly, an animal appeared to stop the chaos at the wedding. On the main stage, there were 4 animals with a total of 10 legs. Which animal among the 12 zodiac signs interrupted the wedding?  🐭 🐮 🐔

Math Olympiad problems for students transitioning from fourth to fifth grade

This is a math competition problem from the fourth to fifth grade level, where you start using fractions to solve the problem. 😙

The number of red bookshelves is 1/3 of the number of green bookshelves. The number of books on each red bookshelf is 1/4 of the number of books on each green bookshelf. Each green bookshelf has 4 books, and there are no 4 red bookshelves in total. How many books are there on the red and green bookshelves in total?

The problem states that there are 4 red bookshelves 🟥🟥🟥🟥, and the number of red bookshelves is 1/3 of the number of green bookshelves.

Therefore, there are 12 green bookshelves. 🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩

🟩Each green bookshelf has 4 books📙📙📙📙, while each red bookshelf has 1/4 the number of books as each green bookshelf.

🟥So each red bookshelf has 1 book📔.

Not too difficult, right? 😁

(Kindergarten Math Olympiad)

Kindergarten Math Olympiad Problems K2

Kindergarten Math Olympiad Problems K3

This is a Level 1 kindergarten math competition problem (preschool math competition). The wedding-related problem below isn't something even adults can solve immediately 😙

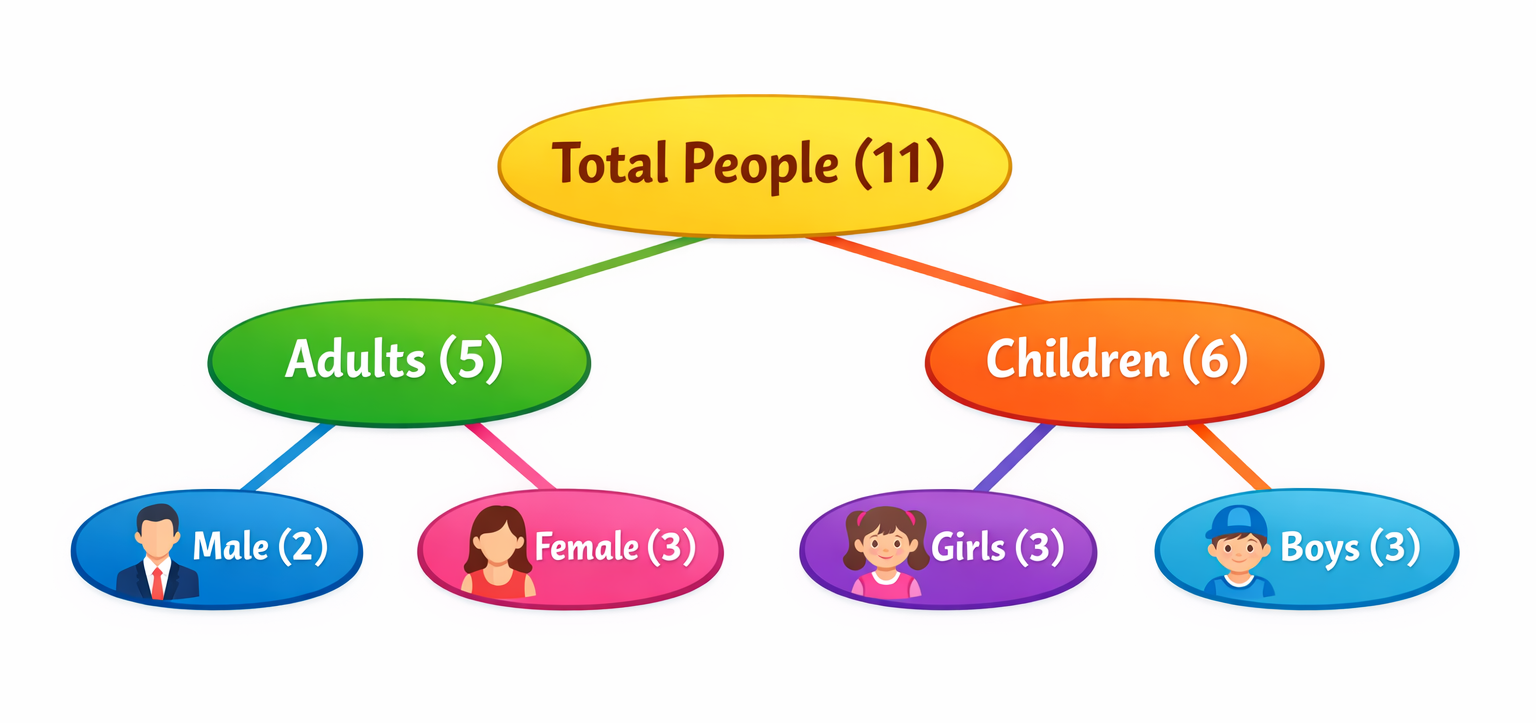
Suki attends a wedding. There were individuals in the wedding, five of whom were adults. Suki found 3 of them girls and 2 male adults. How many female adults are there in the wedding? And how many boys are there?

In our competitive-level math olympiad (preschool math olympiad), we teach children to use different methods to try and deduce the answer. ✨

We can have the kids draw a table, with boys on the left and girls on the right, adults on top and children on the bottom, then insert the relevant numbers to deduce the answer. 😉

Other articles:

1. [What is Olympiad Math?] Breaking down 4 reasons why Olympiad Math can make children "outstanding".

2. [Olympiad Math Problems] Free download of Olympiad Math practice problems detailed video explanations (Part 1)

3. Children's math is not good? 5 tricks to help him improve number sense, strengthen the foundation

4. International School Math | Hong Kong's Only English-Language Math Olympiad | International School Math

5. [Olympiad Math Problems] Free download of Olympiad Math practice problems detailed video explanations (Part 2)

6. STEM Education: The Key to Giving Children a Head Start

7. What is STEM education? Recommendations for STEM interest classes

8. [Children's Extracurricular Classes] Five Recommended Children's Extracurricular Classes: The Key to Giving Your Child a Head Start

9. [Extracurricular Classes for Three-Year-Olds] 3 Must-Take Extracurricular Classes Recommended to Prepare You for Future School Admission Interviews

0. [Five-Year-Old Extracurricular Classes] 3 Must-Attend Extracurricular Classes Recommended to Prepare for Future Math Competitions and Primary One Admission

a. [Four-Year-Old Extracurricular Classes] 3 Must-Attend Extracurricular Classes Recommended to Prepare You for Future School Admission Interviews and Math Competitions