Cultivar el interés de los niños por las matemáticas es un aspecto clave del aprendizaje para muchos padres, y resolver problemas de matemáticas de las Olimpiadas puede mejorar eficazmente el pensamiento lógico y la capacidad de resolución de problemas de los niños. De hecho, las matemáticas de las Olimpiadas no son solo para estudiantes superdotados. Incluso los niños con un rendimiento promedio pueden desarrollar gradualmente su sentido numérico y confianza practicando los problemas de matemáticas de las Olimpiadas progresivamente, desde el nivel elemental hasta el avanzado, comenzando con problemas más sencillos para primero, segundo, tercer y quinto grado. Este artículo recopila diversos recursos para descargar problemas de matemáticas de las Olimpiadas, acompañados de explicaciones en video, lo que permite a los padres acompañar fácilmente a sus hijos en la práctica de las matemáticas de las Olimpiadas en casa.
Estudiar para la Olimpiada Internacional de Matemáticas (OIM) es un método muy eficaz. La OIM no solo requiere que los estudiantes comprendan a fondo conceptos matemáticos complejos como álgebra, geometría y teoría de números, sino que también cultiva su capacidad para resolver problemas. Este aprendizaje también ayuda a desarrollar el pensamiento lógico de los niños, permitiéndoles pensar de forma independiente y creativa, y resolver problemas. Estas habilidades de pensamiento lógico son invaluables en la vida diaria y la investigación académica.
Actualmente existen diversas clases de matemáticas olímpicas y programas de matemáticas olímpicas para preescolares, que permiten a los niños participar y desafiarse con problemas matemáticos olímpicos. A continuación, se presentan algunas recomendaciones de clases de matemáticas olímpicas populares: [Información sobre clases de matemáticas olímpicas populares].
Problemas de la olimpiada de matemáticas de jardín de infantes
Este es un problema de competición de matemáticas de nivel 1 (para preescolares). Los problemas relacionados con la boda que aparecen a continuación son tan desafiantes que incluso los adultos podrían no ser capaces de resolverlos de inmediato. 😙
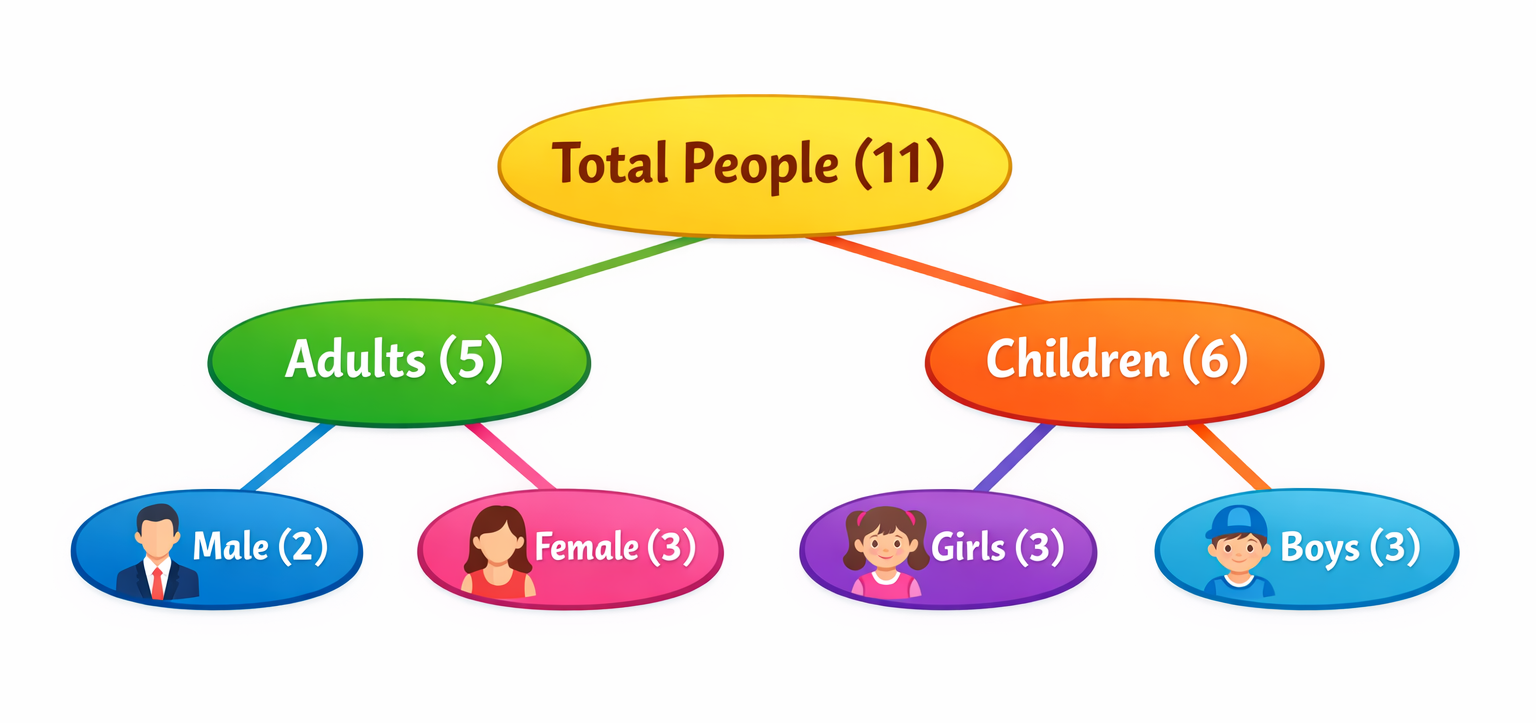
Suki asiste a una boda. Había personas presentes, cinco de ellas adultas. Suki encontró a tres niñas y dos hombres adultos. ¿Cuántas mujeres adultas hay en la boda? ¿Y cuántos niños?

Problemas de la Olimpiada de Matemáticas de K3 a 1.er grado de Primaria
Este es un problema de Olimpiada de Matemáticas de nivel K3 (para preescolares) de la serie de Olimpiadas de Matemáticas de nivel competitivo. El siguiente problema, sobre una ranita saltando, es un ejercicio introductorio de álgebra. 😙
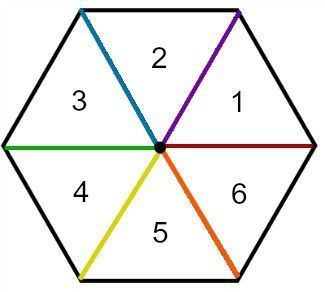
El señor Rana puede saltar en un pie, caminar o saltar en ambos pies.
¿Hasta dónde puede llegar el señor Rana si:
¿Saltar en un pie, caminar y saltar en dos pies?
¿Saltar en un pie, saltar en un pie, saltar en dos pies y saltar en un pie?

En nuestra olimpiada de matemáticas de nivel competitivo (olimpiada de matemáticas de jardín de infantes), enseñamos a los niños a usar diferentes métodos para intentar deducir la respuesta. ✨
Podemos hacer que los niños dibujen una tabla, con los niños a la izquierda y las niñas a la derecha, los adultos arriba y los niños abajo, luego insertar los números relevantes para deducir la respuesta. 😉
En nuestras clases de olimpiadas de matemáticas de nivel competitivo, no utilizamos la memorización mecánica; en cambio, ayudamos a los niños a comprender diferentes conceptos matemáticos, como el álgebra. ✨
¿Saltos, pasos y saltos?
El niño necesita convertir cada acción en un número calculable, por ejemplo, Saltos = 2
Así, podemos conseguir las siguientes oraciones numéricas: 2 1 3 = 6 😉
(Olimpiada de matemáticas de jardín de infantes)
Problemas de la Olimpiada de Matemáticas de K2 a K3
Este es un problema de competición de matemáticas de nivel K2-K3 (competiciones de matemáticas preescolares). El siguiente problema matemático requiere que los niños comparen las cantidades de cebras y jirafas. ¿Puede tu hijo/a hacer una comparación sistemática? En el siguiente problema matemático, ¿cuál es más numerosa, las cebras o las jirafas, y en qué proporción? 😙

En nuestra olimpiada de matemáticas de nivel competitivo (olimpiada de matemáticas de jardín de infantes), enseñamos 48 herramientas de cálculo y guiamos a los niños a usar eficazmente herramientas como Block Model para mejorar la precisión e identificar fácilmente los errores. ✨
Este tipo de problema matemático se puede resolver emparejando dos animales con el método de "encuentra un amigo". El animal que no encuentra un amigo es el que tiene más, y la diferencia es la cantidad entre ellos.
De esta manera podemos obtener la siguiente oración numérica: 5 - 2 = 3 😉
Problemas de olimpiadas de matemáticas para estudiantes en transición de primero a segundo grado.
Este es un problema de competencia de matemáticas para estudiantes de primero a segundo grado. El problema requiere que los niños dividan 6 tarjetas numéricas en tres grupos, asegurándose de que la suma de los números en cada grupo sea la misma. ¿Qué método puedes usar fácilmente para resolverlo? 😙
Hay 6 cartas sobre la mesa. Ella, Tommy y Sarah reciben 2 cartas cada uno. ¿Cuáles son los tres conjuntos de cartas si la suma de los números de todas las cartas en sus manos debe ser la misma?

En nuestras clases competitivas de olimpiadas de matemáticas, enseñamos conceptos matemáticos muy prácticos, como operaciones relacionadas. Al usar con destreza la suma, la resta y la relatividad, podrás encontrar fácilmente las respuestas. ✨
Primero, divide los números en dos grupos según su tamaño: un grupo grande (6, 7, 8) y un grupo pequeño (3, 4, 5), y ordénalos del mayor al menor.
Empareje el número más grande (8) del grupo más grande con el número más pequeño (3) del grupo más pequeño.
8 3 = 11
Empareje el número más pequeño (6) del grupo más grande con el número más grande (5) del grupo más pequeño.
6 5 = 11
Empareje el número del medio del grupo más grande (7) con el número del medio del grupo más pequeño (4).
7 4 = 11
¿Lo entiendes? 😉
(Olimpiada de matemáticas de jardín de infantes)
Problemas de Olimpiada de Matemáticas para estudiantes en transición de segundo a tercer grado
Este es un problema de competencia de matemáticas de segundo a tercer grado, donde usaremos técnicas de razonamiento de más alto nivel para encontrar el peso y la edad de los tres hermanos. 😙
Alex, Benny y Chris son tres hermanos de 20, 19 y 15 años, con un peso combinado de 154 kg. Benny pesa 45 kg. El hermano más delgado pesa 7 kg menos que el más pesado. Chris pesa más que un niño de 19 años, y Alex pesa menos que un niño de 20 años. ¿Cuál es su peso individual?



✨Primero, debemos descartar que Benny sea el más pesado, ya que 45 45 45 > 154 kg
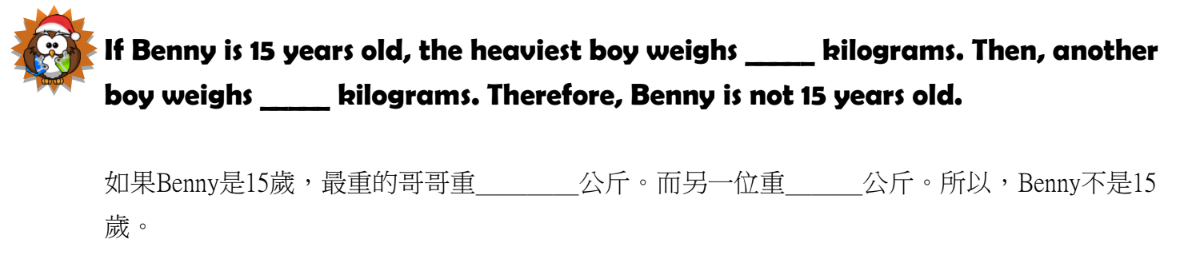
Si descartamos que Benny tenga 15 años, y el hermano más pesado pesa 52 kg (45 7), mientras que el otro pesa 58 kg (58>52), entonces Benny no tiene 15 años.

Tras restar a Benny, los dos hermanos restantes pesan un total de 109 kg (154-45). El joven de 15 años pesa 51 kg, mientras que el más pesado pesa 58 kg.
¿Lo entiendes? 😉