【Math Olympiad Problems】Free Download of Math Olympiad Exercises Detailed Video Explanations

Cultivating a child's interest in mathematics and improving their mathematical skills have always been a major concern for parents. Mathematical Olympiads (OMs) are a highly effective way to achieve this. These Olympiads not only challenge students to gain a deep understanding of complex mathematical concepts such as algebra, geometry, and number theory, but also cultivate their problem-solving skills. This learning process also fosters logical thinking, enabling them to think independently, creatively, and solve problems. These are invaluable logical thinking skills for both daily life and academic study.

Mathematical Olympiad problems are often quite challenging, but when children successfully solve these difficult problems, they gain a great sense of accomplishment and confidence. This experience of success helps motivate children to continue learning and achieve further success in other areas. Overall, studying Mathematical Olympiads not only helps build a solid mathematical foundation but also cultivates important logical thinking skills, while also boosting their confidence and expanding their knowledge.

There are now a variety of Olympiad classes and preschool Olympiad programs available, allowing children to participate in and challenge themselves with math problems. Here are some popular Olympiad class recommendations: [Provides information on popular Olympiad classes].

Kindergarten Mathematical Olympiad Questions

This is a Level 1 Math Olympiad question (for preschoolers). The following wedding-related question is difficult for adults to answer immediately. 😙

In the competition-level Mathematical Olympiad (Kindergarten Mathematical Olympiad), we will teach children to use different methods to try to deduce the answer✨

We can ask the children to draw a table, put the boys on the left and the girls on the right, put the adults on top and the children on the bottom, and then insert the relevant numbers, and we can deduce the answer 😉

In competition-level Mathematical Olympiads, we don’t just drill students mechanically, but instead help them understand different mathematical concepts, such as Algebra.

Hops, steps, and jumps ?

Children need to convert each action into a calculable number, e.g. Hops = 2

This allows us to achieve the following Number Sentence: 2 1 3 = 6 😉

(Kindergarten Mathematical Olympiad)

Mathematical Olympiad questions for K2 to K3

This is a K2 to K3 math problem from the competitive math Olympiad (Kindergarten Math). The following math problem requires children to compare the number of stag beetles and giraffes. Can your child make this comparison systematically? In the math Olympiad picture below, which one is more numerous, stag beetles or giraffes? How much more? 😙

In our competition-level Mathematical Olympiad (Kindergarten Mathematical Olympiad), we will teach 48 types of calculation tools and teach children to effectively use tools such as Block Model to improve accuracy and make it easier to find mistakes✨

For this type of math problem, we can pair the two animals using the "find friends" method. The one that cannot find a friend is the "larger one", and the extra one is the difference in number.

This allows us to achieve the following Number Sentence: 5 - 2 = 3 😉

Mathematical Olympiad questions for the transition from grade one to grade two

This is a competition-level math Olympiad problem for children in Grade 12. It requires children to divide 6 number cards into three groups, and make the sum of these groups the same. How can you easily do this?

In our competition-level Mathematical Olympiad, we will teach some very practical mathematical concepts such as Related Facts. By making good use of addition and subtraction, you can easily find the answer.

First, divide the numbers into 2 groups, large group (6,7,8) and small group (3,4,5), and arrange them from large to small.

Pair the largest number in the large group (8) with the smallest number in the small group (3).

8 3 = 11

Pair the smallest number in the large group (6) with the largest number in the small group (5).

6 5 = 11

Match the middle number of the large group (7) with the middle number of the small group (4).

7 4 = 11

Get it? 😉

(Kindergarten Mathematical Olympiad)

Mathematical Olympiad questions for the transition from second grade to third grade

This is a competition-level math Olympiad question for the sophomore to junior year classes. We will use the most advanced reasoning skills to find the weight and age of three brothers.

✨First, we need to exclude Benny as the heaviest, 45 45 45 > 154Kg

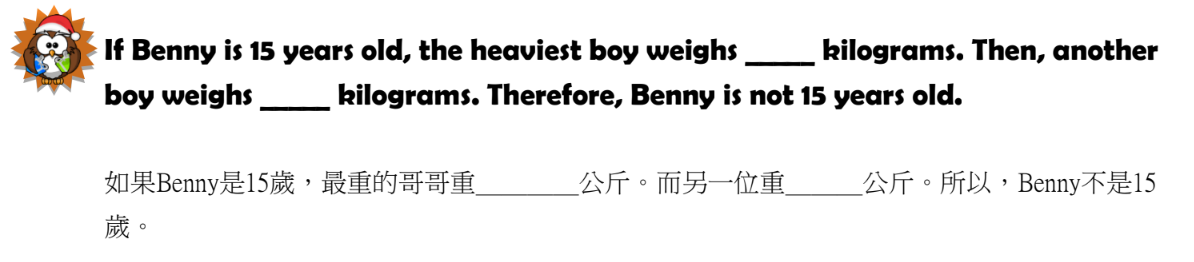
So we can rule out Benny being 15 years old. If the heaviest brother weighs 52 kg (45 7) and the other weighs 58 kg (58 > 52), then Benny is not 15 years old.

After deducting Benny, the remaining two brothers weighed a total of 109 kg (154-45). The 15-year-old weighed 51 kg, and the heaviest weighed 58 kg.

Get it? 😉

Other articles:

1. [What is Mathematical Olympiad] 4 Reasons Why Mathematical Olympiads Can Make Children More "Excellent"

2. [Math Olympiad Problems] Free Download of Math Olympiad Exercises Detailed Video Explanations (Part 2)

3. [Olympiad Class Recommendations] Unveiling the Mysteries of Hong Kong's Five Major Mathematical Olympiad Courses!

4. International School Math | Hong Kong's only English-language Mathematical Olympiad course | International School Math

5. STEM education: The key to giving children a head start

6. What is STEM education? Recommended STEM interest classes

7. Children's math is not good? 5 tricks to help him improve number sense, strengthen the foundation

8. [Three-Year-Old Interest Classes] 3 Must-Take Interest Classes to Prepare for Future College Interviews

9. [Children's Interest Classes] Five recommended children's interest classes, the key to your child's success at the starting line